パレート最適なサロゲート群を利用する適応サロゲート進化計算
概要
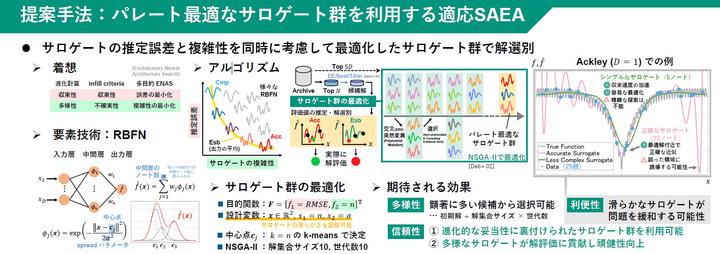
機械学習により解評価を代替するサロゲート進化計算(SAEA)では,最適化性能はサロゲートの性能に依存するため,これを適切に選択することが重要である.近年では,一回の最適化プロセス中にオンラインにサロゲートを選択する適応SAEAが盛んに研究されている。既存の適応SAEAでは,目的関数値に対する推定誤差などの近似精度指標でサロゲートを選択することがほとんどである。しかしながら,目的関数を忠実に再現することのみが重視された結果,多数の局所解を持つサロゲートが構築され,探索を不要に困難にしている可能性がある.そこで本研究では,近似関数の滑らかさに変化を与えるパラメータを変化させながら,近似精度とサロゲートの複雑性の両方を考慮したサロゲートの選択法を提案する.具体的には,提案法では,近似精度とサロゲートの複雑性を2目的最適化問題とみなし,多目的進化計算でパレート最適なサロゲート群を得る.次に,近似精度の高いサロゲートと,滑らかに近似して問題を易化したサロゲートの両方を活用して,解評価する解を選別する.実験では,CEC2013ベンチマークセットで提案手法が最先端のSAEAよりも優れた性能を導出することを示す.
文献種別
収録
第17回進化計算シンポジウム講演論文集, pp. 380–387
参考
- 本サイトの全ての添付ファイルは著者バージョンであり,出版バージョンと一致しない可能性があります.