Competitive-Adaptive Algorithm-Tuning of Metaheuristics inspired by the Equilibrium Theory: A Case Study

概要

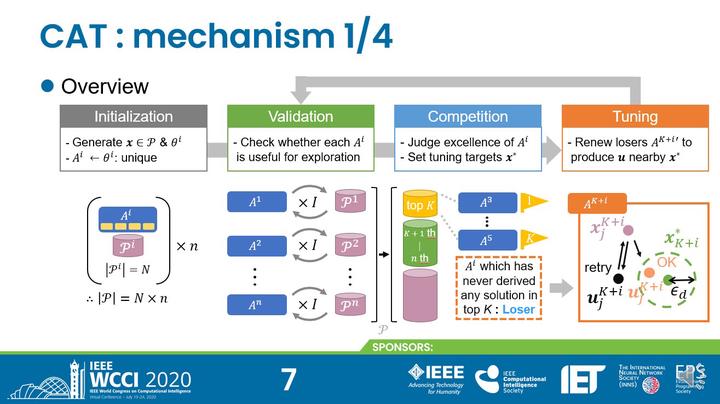
This paper proposes a competitive-adaptive algorithm tuning framework for meta-heuristic algorithms. Our proposed method, called CAT, is inspired by the Equilibrium Theory in economics, which explains competitors eventually converge to an equilibrium status, e.g. in terms of the price of products. In detail, our proposal runs multiple optimizers with different algorithmic configurations, e.g. mutation variants. Then, the configurations of inferior optimizers are adaptively tuned so that they can derive good solutions that superior ones have derived. This intends to boost the performance even with a limited number of fitness evaluations, by the following technical advantage. The CAT preliminarily validates a search capacity of tuned algorithmic configurations and then constructs an ensemble optimizer by utilizing multiple optimizers. As a case study, this paper applies the CAT to tune the differential evolution algorithms (DEs). Experimental results show that our proposal outperforms the standard DE and an alternative approach i.e. jDE, which adapts hyper-parameters of genetic operators.