Utilizing the Expected Gradient in Surrogate-assisted Evolutionary Algorithms

Abstract

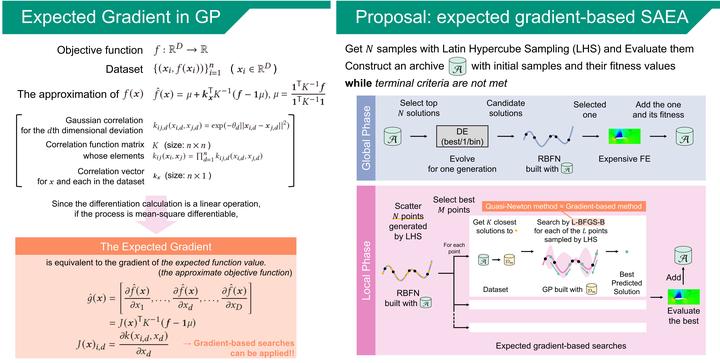
In the field of surrogate-assisted evolutionary algorithms (SAEAs), Gaussian Process (GP) is a widely used technique to approximate the objective function. Although a GP model can provide an expected gradient of a function to be approximated, little attention has been paid to the utilization of the gradient information. Thus, this paper presents an expected gradient-based SAEA, in which the expected gradient of the objective function provided by the GP models is utilized to conduct an efficient local search. Specifically, the proposed algorithm first conducts a global search with a differential evolution algorithm to find promising regions of the search space. Then, it builds a GP model for each promising region, and a quasi-Newton method (L-BFGS-B) is executed on its model with guidance from the expected gradient. This gradient-based local search intends to sufficiently search the approximate objective function, by finding various local optimal solutions in an efficient manner. Experimental results show that our algorithm is competitive with state-of-the-art SAEAs on a single-objective optimization benchmark suite.

Kei Nishihara

2nd-year Doctoral Student

My research interests include evolutionary computation and swarm intelligence.